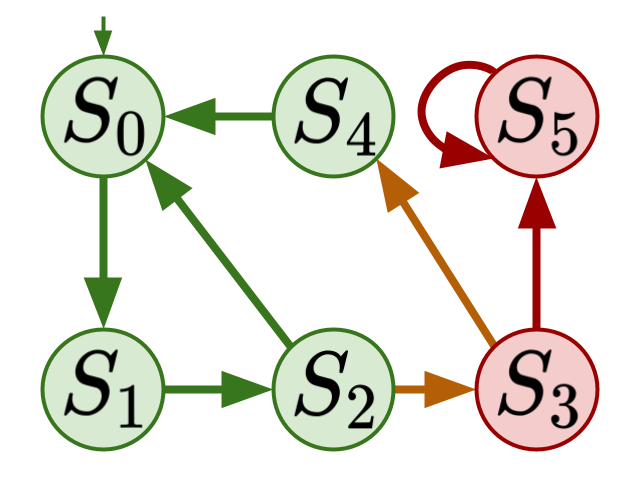
Design-Time Computation of the Recoverability of a System

System Recoverability

Model Checking

Computation Tree Logic

Many software systems are not verified because it is expensive – both financially and temporally – to show a system is 100% correct. Additionally, many systems do not need total correctness; some systems may tolerate property violations as long as they eventually recover. If a property requires that an invariant holds at all times during execution, it may be more important for the system to recover from the invariant violation than for the violation itself to be removed. We analyze systems to compute their recoverability – if an invariant is violated in the system, is it possible to return to a safe state from that violation. Addtionally, we examine different categorizations of recovery; if an invariant is violated multiple times, it may be possible to return to a safe state after some violations, but not others. The actions required to return to safety are also in question, especially if some actions require human intervention to return to safety. A system that can always recover from an invariant violation may be less safe than a completely correct system, but we explore the possibility that it is easier to guarantee recoverability than correctness of a system.